Vir Karan

Vir Karan

PhD Student, UC Berkeley/LBNL | IIT Madras MME '23

Research

Here’s a link to my Google Scholar page. In short, the following key-words describe my research interests:

  1. Computational Materials Science
  2. Deep Learning
  3. Materials Informatics
  4. First principles Modelling of Materials
  5. Solid-State Phase Transformations

Publications

  1. Ashok Allamula, Vir Karan, Peela Lasya, Daljin Jacob, Parasuraman Swaminathan, and Satyesh Kumar Yadav. “Optimization of the deposition process parameters of DC magnetron sputtering to achieve desired deposition rate using design of experiment method.”, Journal of Electronic Materials (2023) [Full-Text] (*-contributed equally)

  2. Sanket Thakre, Vir Karan, and Anand K. Kanjarla. “Quantification of similarity and physical awareness of microstructures generated via generative models.” Computational Materials Science 221 (2023): 112074. [Full-Text]

  3. Vir Karan, A. Maruthi Indresh, and Saswata Bhattacharya. “Accelerated Solutions of Coupled Phase-Field Problems using Generative Adversarial Networks.” arXiv preprint arXiv:2211.12084 (2022). [Pre-Print PDF]

Projects

I’ve worked primarily on data-driven methods to model materials, and the following is a very brief description of some of the projects I’ve worked on. You can use the key words that I’ve highlighted under each project to know more about the methods used, or just shoot me an email!

  1. Optimization of Silver thin film characterisitcs using design of experiments (Key words: Taguchi designs, response surface model fitting, desirability function based optimization)
    • Silver is a common materials used for coatings, especially in electronic applications due to its high conductivity. However, most coatings don’t need to be excessively thick to show the desired amount of conductivity. Hence, there are usually two competing objectives when synthsizing silver based thin films: a) maximize the conductivity of the deposited film, b) reduce the amount of silver being deposited to reduce cost and processing time.
    • I worked on depositing films for a varying set of processing parameters using DC Magnetron sputtering, and finding the right balance between these objectives using tools from the design of experiments.
    • This was the first experimental project that I’ve worked with, and it’s warming to know that my contribution was significant enough to get my name on a publication for this work as well!
  2. Morphology optimization of DP Steels using GANs and U-nets(Key words: Generative deep learning, image-to-image translation, digital microstructural optimization)
    • In the past, there have been several ML based surrogates fitted for computing the stress/strain fields in materials given the material’s microstructure. However, there was a lack of a solid design framework that could leverage such models to actually design materials. I had worked with generating digital microstructures earlier using Generative Adversarial Networks (GANs). The neat thing about GANs is that they can act as effective dimensionality reduction models, and so a GAN can give a much lower dimensional “latent code” for a material’s microstructure.
    • I worked with attempting to link these “latent codes” with actual physical properties (such as tensile damage resistance), and using a bayesian optimization routine to design microstructures. This worked involved me learning how to use Abaqus and perform FEM simulations of 2-phase materials, and then fitting U-net based surrogates to bypass the same FEA, and linking the trained surrogate to the GAN’s outputs.
    • This work was done as part of the Young Research Fellowship at IIT Madras, and resulted in me delivering a poster presentation on the same on 19th August 2022 at IIT Madras as part of the YRF Showcase ‘22.
  3. Phase-field modelling of Al-Zn alloys using grand potential formulations(Key words: Phase-field methods, CALPHAD-coupled modelling of phase transformations, grand-potential formulation of phase-field problems)
    • The microstructure of a material dictates several macroscopic properties of materials, and it is possible to predict the morphology (what phases are present in the material and how they are distributed) using phase-diagrams and thermodynamics. However, it is important to understand how the microstructure of materials evolve when they are put under different processing conditions (such as during heat treatments and during service). One way to do this is using simulations, specifically using Phase-Field Modelling.
    • This work was my first project dealing with phase-field models, and computational modelling in general. I worked on firstly extracting thermodynamic data for Al-Zn alloys through pyCALPHAD (a python fork for using CALPHAD databases), and then wrote C codes to solve the phase-field equations (Cahn-Hilliard and Allen-Cahn) for a variety of phase transformations (spinodal decomposition, isotropic precipiate growth, dendritic solidification).
    • I then worked on reformulating the phase-field problem using the chemical potential as the independent variable of the problem (thereby formulating the kinetics in terms of the driving force of the transformation), using what’s called the “Grand Potential Formulation” of phase-field problems. I then performed the same set of simulations using the reformulated equations. What made this challenging is that the reformulation works like a charm when the free energy well of the material is purely convex in nature. In the case of Al-Zn, the free energy has a double-well shape for the non-terminal phases, leading to the chemical potential not being uniquely defined.
    • I was able to do the simulations for spinodal decompistion and precipiate growth, but couldn’t finish the same for the solidification problem. I did get a lot of really cool GIFs of phase-field simulations in the process though, so not a total loss (check the GIF at the bottom of this page :))
  4. Accelerated solution of phase-field problems using neural networks (Key words: Phase-field methods, neural operators, generative deep learning, physics-informed neural networks)
    • Most modelling problems (such as phase-field or fluid dynamics problems) tend to deal with solving a set of strongly coupled PDEs, which is a numercially difficult task. Hence, there has been a lot of research into developing new methods for this task, and of late neural networks have been shown to be promising surrogates.
    • I first worked on this domain for a phase decomposition problem in a ternary alloy, for which I implemented a custom GAN-type network, alongside a fourier neural operator. Both of these models were quite effective in learning the “operator” behind the phase-field PDEs, and for this work I wrote my very first (first-authored) paper!
    • I worked on another phase-field problem (modelling a stress-induced martensitic phase transformation) during my MITACS internship during the summer of 2022. The actual phase-field problem is more complicated, since it involves coupling the equations of mechanical equilibrium to the Allen-Cahn equation. I was able to solve a simple variant of this problem using finite differences, and successfully fit a Physics-Informed Neural Network (PINN) for the same. For complicated loading conditions and anisotropic elastic properties however, the PINN training did not converge, which unfortunaely is a known flaw of this modelling approach.

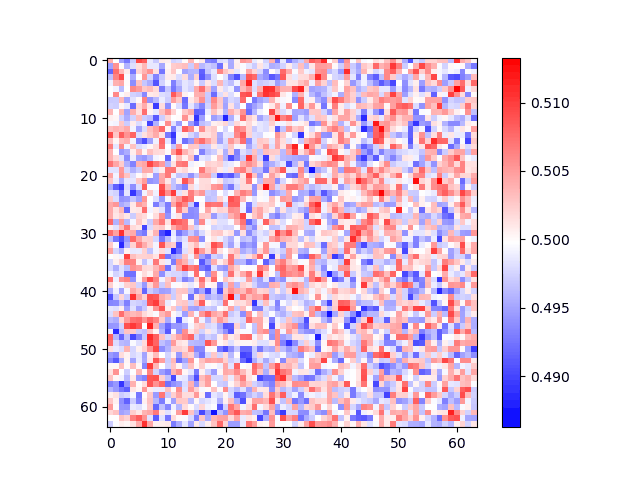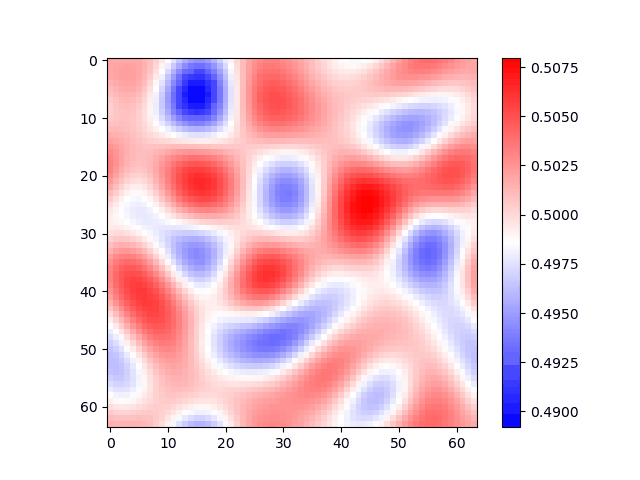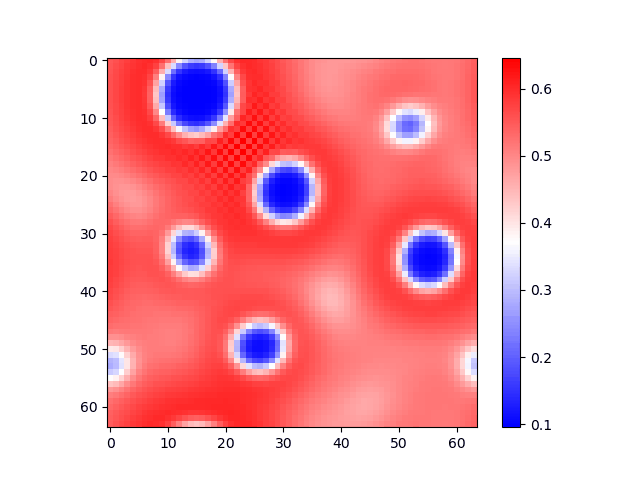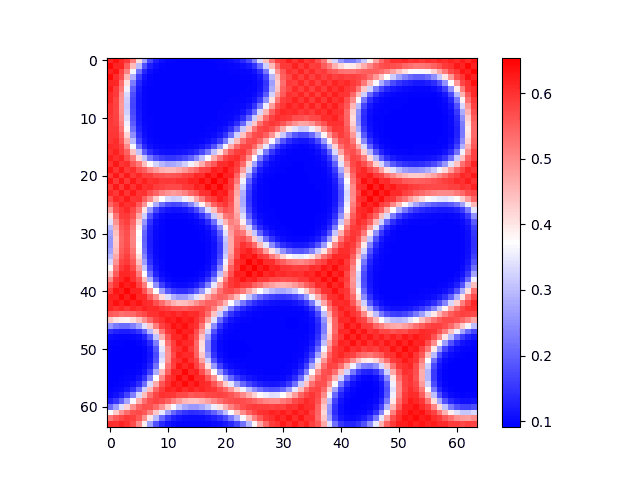
Phase-Field simulation of a phase deomposition transformation in an undercooled Al-Zn melt!

Phase-Field simulation of a phase deomposition transformation in an undercooled Al-Zn melt of equal initial concentrations of Al and Zn. Initially there is diffusion across the domain, followed by nucleation and growth of two compositionally different phases (Red and Blue).